Figure 1: Notable relationships between nodes
Tsurgeon (Levy and Andrew 2006) is a software tool for changing bracketed (Penn) style trees with tree search patterns paired to tree editing actions. This guide shows how to write tree changing programs with examples of basic and advanced use. Explanatory detail comes from README-tsurgeon.txt, which is part of the Tregex distribution that includes Tsurgeon. For the discussion of Tregex patterns, there is also inclusion of explanation from the TGrep2 manual that accompanies the TGrep2 (Rohde 2005) search tool.
Tsurgeon (Levy and Andrew 2006) is a software tool for changing bracketed (Penn) style trees. It follows directions of a program written as a series of pairings of a Tregex pattern for matching tree structure with tree editing Tsurgeon action(s). It works by taking trees specified with round bracketed notation as input. With each input tree, it tries to match Tregex patterns to the tree. For each successful pattern match, it applies editing actions until the activating match no longer holds true. Resulting trees are printed as a final output after all pattern and action pairings have been applied in turn to each input tree.
This guide is structured as follows. Section 2 details the required format for Tsurgeon programs that consist of one or perhaps many pairings of a Tregex pattern with Tsurgeon action(s). Section 3 sketches the workings of a full example. Section 4 details Tregex patterns. Section 5 demonstrates in turn each of the available Tsurgeon actions. Section 6 presents an extended example.
Tsurgeon programs are a combination of a Tregex pattern to match input trees and a series of Tsurgeon actions to perform on matched trees. The Tsurgeon program is unforgiving about the required line formatting of a program, because this is how Tregex patterns are distinguished from Tsurgeon actions. In particular:
Program 1 is an example of a correctly formatted program:
When Tsurgeon runs your program, it will read in each tree of the input, one after the other. Each time it reads in a tree, it will see if your Tregex pattern finds a match. If it does, then it will keep performing the Tsurgeon action(s) for the active Tregex pattern, stopping only when the Tregex pattern no longer matches. You can define as many pairings of a Tregex pattern with Tsurgeon action(s) as you like. If more than one pairing occurs, each pairing is performed in the order they appear in your program. So Tsurgeon is, in effect, three nested loops: from the input go over the trees; for each tree go over the patterns and, if a Tregex pattern matches, keep going over the Tsurgeon action(s), until there is no longer a match for the Tregex pattern.
To see program behaviour, consider Program 1 of section 2. The first noncomment line, repeated as (1), specifies with a Tregex pattern the initial tree structure looked for.
See section 4 for details about Tregex patterns. Here it is enough to know that (1) finds trees when there is a node such that it:
For example, tree (2) is matched:
Nodes of a found tree are named when ‘=
The Tsurgeon action for the first Tregex pattern, repeated as (3), is given on the third line of the program, which follows an empty line.
This tree transforming action brings about a relabelling to WORD of the node referred to with ‘x’ following the match with pattern (1). The combination of this initial Tregex pattern and Tsurgeon action is to transform the example matched tree (2) into (4).
Note how (4) is reached by action (3) being applied twice, after which pattern (1) is no longer able to find a match.
Following action (3), there are then two empty lines in Program 1, making line 6 that follows a new pattern to find trees that contain a node name that matches the simple string pattern WORD which can thereafter be referred to with ‘x’. There is then another empty line, making line 8 that follows a Tsurgeon action to remove the node referred to with ‘x’, resulting in (5) as the overall output from running the program of Program 1 on the input tree (2).
By first changing all words to WORD and then removing all WORD instances, Program 1 demonstrates how the match of a Tregex pattern with Tsurgeon action(s) will apply repeatedly until no further match is possible. Attractive consequences of this runtime behaviour are that trees may match Tregex patterns multiple times, and earlier Tsurgeon actions may enable subsequent matches of the active Tregex pattern for further Tsurgeon actions. But with such power comes responsibility: Extra special care is needed to avoid starting an infinite loop. For example, consider missing the initial ‘!’ (negation) sign from the first pattern of Program 1, to give Program 2:
The changed pattern will find terminal nodes that are not dominated by nodes beginning with PU, and that are either WORD or character strings that begin with ‘*’. This pattern will match the same tree (2) as seen with the discussion of Program 1, while now it is the occurrence of * that is changed to WORD, resulting in (6).
The transformed tree of (6) continues to match the triggering pattern because of the presence of WORD resulting in the replacement of WORD for WORD, which continues to match, and so the loop of changing WORD into WORD continues with no termination prospect.
Patterns are expressed with the Tregex pattern language. This closely resembles the query language of TGrep (Pito 1994), the original tree-matching program that came with the Penn Treebank, and includes extensions from TGrep2 (Rohde 2005), another TGrep-like implementation. Notably:
Single tree nodes are matched as follows:
Tregex regular expressions follow Java conventions for expressing regular expressions. For details, see: https://docs.oracle.com/javase/7/docs/api/java/util/regex/Pattern.html.
Specified as a string, a regular expression matches a node if there is a part of the node that is matched. For example, /[PCV]P/ matches PP, CP-THT, ADVP, etc.
The caret (‘^’) anchors the regular expression to the beginning of a matched node. So, /^[PCV]P/ will not match ADVP but will match PP and CP-THT. A dollar sign (‘$’) as the last character will anchor the regular expression to the end of a matched node. For example, /PRD$/ will not match NP-PRD2 but will match NP-PRD. Use of both the caret and dollar-sign in /^[NP]P$/ constrains the match to only NP and PP. A regular expression can also be constrained with ‘\b’ to mark a word boundary. Thus, /^NP\b/ will match NP and NP-PRD but will not match NPR.
By default, regular expressions are case sensitive and so /^The$/ and /^the$/ match different nodes. Case insensitivity can be turned on by including the flag (?i) and then everything to the right will be case-insensitive, e.g., /^(?i)the$/ matches: THE, The, the, tHE, etc. Having turned case insensitivity on, it is possible to turn case insensitivity off with the flag (?-i) to become case sensitive again, e.g., /^t(?i)h(?-i)e$/ matches: the, tHe. It is also possible to limit the region of case insensitivity to a given variable group (see section 4.5), e.g., while /^t(h)e$/ matches: the, /^t(?i:h)e$/ matches: the, tHe.
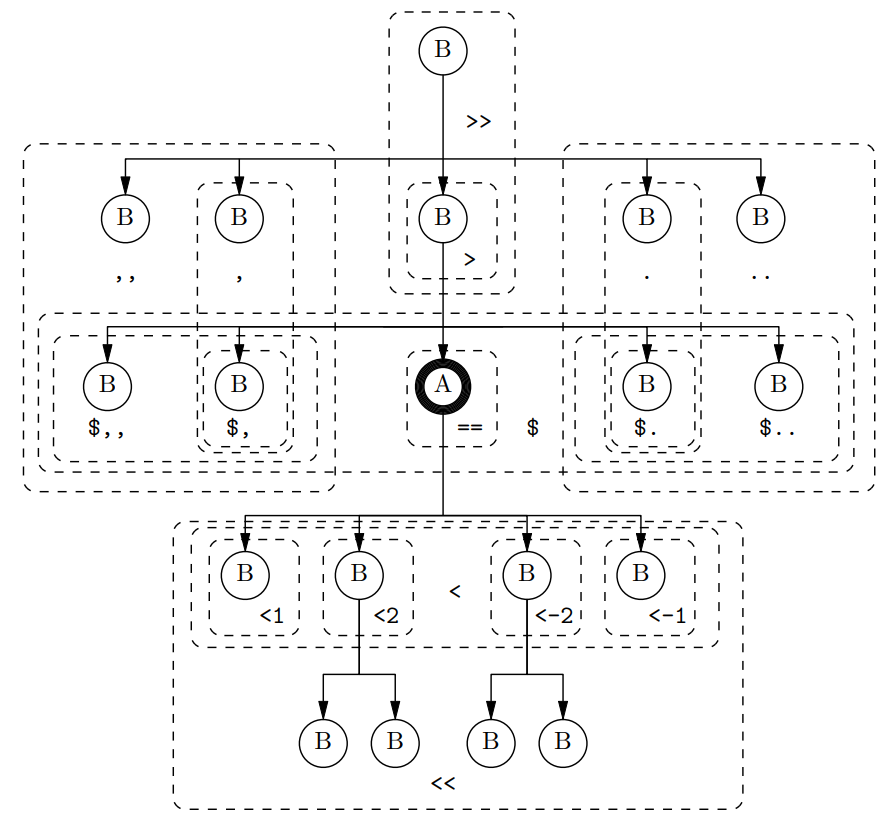
Relationships define connections between nodes. There is a complete pairing of relationships with counterparts, allowing for flexibility when constructing complex relationships (see section 4.3). Notable relationships can be pictured as in Figure 1.

The relationships pictured in Figure 1 are described in (7).
To specify the exact child position which a node must (or must not) occupy, use the i-th child relationships (<i, <-i, !<i, and !<-i; also expressed with >i, >-i, !>i, and !>-i). In these relationships, i represents a number indicating which child ‘slot’ is to be considered. Positive numbers are counts from the left edge, while negative numbers are counts from the right edge. For example, (8) finds instances of NP where the second child is a PP.
Pattern (9) finds instances of NP where the last child is a PP.
Pattern (10) finds instances of NP which have less than three children. That is, every NP which has three or more children will have something as its third child to make matching with (10) fail.
To select nodes with specific numbers of children you can use a positive and negative i-th child relationship. For example, to find NP nodes which dominate either two or three children you would use pattern (11):
Other available relationships between nodes, additional to those given above in (7), are given in (12):
Complex Tregex patterns can be constructed by specifying Boolean expressions of relationships that connect to a node. If no operator is placed between two relationships, they are assumed to be connected by an and, which can be specified for clarity with an ampersand (‘&’). Thus, patterns (13) and (14) both match an IP node which immediately dominates a PP node and which dominates an IP node.
The second relationship ‘<< /^IP\b/’ refers to the first IP and not to the PP, and is equivalent to (15).
The placement of parenthesis can be used to group a node with its relationship(s), so that (16) will match an IP which immediately dominates a PP which in turn dominates some IP.
If a pipe (‘|’) is placed between two relationships, only one of the relationships must be satisfied. Pattern (17) will find an IP node which immediately dominates a PP node or dominates an IP node:
The (possibly implicit) and binds tighter than the or. So pattern (18) will find an IP node that has VB and VB2 children or that has NP-PRD and AX children.
To create more complex expressions, square brackets (‘[]’) can be used to group relationships to form a complex relationship. Thus, pattern (19) finds an IP that has a VB or NP-PRD child, and that precedes a subject sister or follows an ADVP sister.
Because a square bracketed expression itself acts as a complex relationship connecting to a node, an open square bracket must immediately precede a relationship or another open square bracket that itself starts a complex relationship.
Any relationship, including a square bracketed one, can be negated by immediately preceding it with an exclamation mark (‘!’). Thus, pattern (20) will find IP nodes that do not simultaneously have NP and PP children.
As seen with the deprogramion in section 3 of Program 1, Tregex patterns allow for a matched node to be given a unique label with an equal sign (‘=’) and then referred to by that label when Tsurgeon actions are triggered. It is also possible to use labels to refer to other nodes from within the Tregex pattern. Such a ‘back link’ is accomplished when the node name only consists of an equal sign and a label, with the label serving to refer to the node that has been assigned to that name elsewhere in the pattern. It is only possible to express patterns in which the labeled node comes prior in the connected structure of the pattern that leads to a back link.
Having back links leads to the creation of patterns with cycles in the link structure. For example, imagine we wanted to find a clause node, /^IP\b/, that dominates a clausal complement, /THT/, and a /^PP\b/, such that the /THT/ precedes the /^PP\b/. This requires stating relationships between the /^IP\b/ and the /THT/, between the /^IP\b/ and the /^PP\b/, and between the /THT/ and the /^PP\b/. With access to labels, the query can be written as (21).
The /^IP/=foo matches any tree node whose name begins with IP. Furthermore, when a matching tree node is found, it is given the label foo. Later, ‘/^PP\b/ >> =foo’ indicates that the PP must be dominated by that very same node, not just any IP.
As another example of how back links are useful, consider the task of finding relative clauses with object traces. An object trace might be embedded arbitrarily deeply inside its relative clause, which is captured with the dominates relation (‘<< (/OB1/ < /\*T\*/)’). However, without further qualification, this is too liberal, as it will also allow the return of a relative clause that itself has no object trace but contains a relative clause with an object trace. We can add the extra qualification to prohibit the unwelcome scenario with a back link, resulting in (22).
The added back link statement (‘!>> (/REL/ >> =p)’) requires there to be no intervening relative clause (/REL/) between the object trace and the relative clause that the pattern serves to find.
If you write a node deprogramion using a regular expression, you can assign its matching groups, established with round brackets internal to the regular expression, to variable names. The syntax is:
If more than one node has a group assigned to the same variable name, then matching will only occur when all such groups capture the same string. For example, pattern (24) will find identical adjacent terminal nodes (reduplicated words).
Nodes matched with (24) have to be terminal because of the ‘!< __’ conditions that state how there can be no children, and adjacent because of the dot (‘.’). With ‘#1’, word takes its value to be the first group in the regular expression, which is the word that needs to have occurred twice in a row.
A major use of naming variable groups is to carry over named content into the relabel Tsurgeon action that is used to relabel node content (see section 5.4).
Tregex patterns can be split into multiple segments, which are separated by colons (‘:’). Segments following the first can begin with a reference to a labeled node that is defined in a previous segment. Thus, pattern (25) will find trees where an NP immediately dominates a CP-THT.
With labeling of complex nodes, segments can entirely replace patterns that otherwise require embedded relationships. For example, tree fragment (26) is matched by pattern (27) without segments as well as pattern (28) with segments.
Segments can make patterns easier to read and debug. Segments can also assist with pattern reuse. Patterns can frequently be mostly the same while differing in only one region. For such cases, the region that changes can be placed in its own segment, so that full patterns are built when a unique segment is appended to a common base, or vice versa.
Segments need not be related. Thus pattern (29) finds trees with an IP-ADV and IP-SUB, without other requirements for how these nodes relate to one another.
Note that the colon has a low precedence, so that (30) matches trees with an IP-SUB that does not immediately dominate a VBP and an IP-ADV that does immediately dominate a VBP.
With the previous section describing Tregex patterns, the current section turns to considering the range of Tsurgeon actions that Tregex patterns can invoke. Legal Tsurgeon actions are as follows:
deleteWe will look at these Tsurgeon actions in turn, with a deprogramion and example(s) for each.
for each <name_i>, deletes the node it names and everything below it.
Program 3 consists of a pattern to find nodes whose label starts with ‘*’ and that do not dominate any other node. This pattern is paired with an action that deletes any matched node.
Input:
Output:
Note that only the matched node, *, is removed, to leave NP-LGS with no child.
for each <name_i>, prunes out the named node. Pruning differs from deletion in that if pruning a node causes its parent to have no children, then the parent is in turn pruned too.
Program 4 has the same pattern as seen with Program 3, but differs in terms of the action being prune.
Input:
Output:
The * node is removed, and since this results in the NP-LGS above it having no terminal children, the NP-LGS node is deleted as well.
The <name1> node should either dominate or be the same as the <name2> node. This excises out everything from <name1> to <name2>. All the children of <name2> go into the parent of <name1>, where <name1> was.
Program 5 begins with the wild card pattern to identify a node that will dominate another node that is picked out with the x name and that will itself dominate at least one node that is dominating another node. The pattern is paired with an excise action that will remove nodes that can be named x from the tree.
Input:
Output:
This example has illustrated returning a flattened version of the input tree, with all non-root non-preterminal and non-terminal level nodes removed.
With Program 5, an action to excise a single node was repeatedly applied. Program 6 illustrates excision of multiple nodes, with all inbetween material also being removed.
With (35) as input, there is output:
From the input, there is repeated elimination of both a PP node and its dominated NP node, as well as all inbetween material, namely, the instances of:
relabels the node <name> to have a new label <new-label>. There are three possible forms for a relabelling instruction to take. The first form, illustrated with (39), is used for changing a node label (namely, nodeX) to an alphanumeric string (namely, NP).
The second form, illustrated with (40), is used for relabeling a node to something that isn't a valid identifier without quoting.
The third form, illustrated with (41), is used for regular expression based relabeling.
The third form lets you make a new label that is an arbitrary String function of the original label and additional characters that you supply. In this last case, all matches of the regular expression against the node label are replaced with the replacement String. This has the semantics of Java/Perl's replaceAll: you may use capturing groups and put them in replacements with $n. For example, if the pattern is /foo/bar/ and the node matched is foofoo, the replaceAll semantics results in barbar. If the pattern is /^foo(.*)$/bar$1/ and the node matched is foofoo, relabel will result in barfoo.
When using the regex replacement method, the form of the regex is limited to literal character strings, the wild card character (‘.’), the Kleene star (‘*’), the string initial marker (‘^’), and the string final marker (‘$’). In order to utilise a more complex regex for use as replacement content, you can use the sequence \%{var} in the replacement string to supply the content of a matched variable group (see section 4.5). You can also use the sequence ={node} in the replacement string to use captured nodes in the replacement string (see Program 8 below). To get a ‘%’ or an ‘=’ or a slash in the replacement, escaping with ‘\’ is necessary, so: ‘\%’, ‘\=’, ‘\/’, and ‘\’.
The pattern of Program 7 will look for a non-terminal node that contains a non-empty substring that is either -TPC or -EPD and that should be preceded by a non-empty substring whose content is captured by the variable group name start and that is followed by a possibly empty substring whose content is captured by the variable group name end. There follows an action that changes the label of the found node so that only the content of start and end remain. Note that ‘^.*$’ (match all string content) of the relabel action is necessary to make sure the regex pattern only matches and replaces once on the entire node label.
Input:
Output:
This example illustrates the content from two variable groups (start and end) being carried over from the matched node to serve as the replacement content.
The pattern of Program 8 will look for a terminal node immediately dominated by an ID node and add the content of this node to every non-terminal node with content that is not ID and that does not already contain the to-be-added content.
Input:
Output:
moves the named node into the specified position. To be precise, it deletes (*NOT* prunes) the node from the tree, and re-inserts it into the specified position. See section 5.7 for how to specify position.
Program 9 demonstrates the promotion of punctuation (PU) to a higher constituent layer when on the left or right edge of a constituent layer (identified as ‘y’) that is dominated by at least one more node, that is, when ‘y’ is not the root node of the tree. The first pattern-action pair covers the left edge scenario, while the second pattern-action pair covers the right edge scenario.
Input:
Output:
Both patterns of Program 10 contain a disjunction with two parts. The first part captures quantifier movement within the same (clause) layer. Here, the pattern involves a relation of sisterhood and precedence (‘$..’) to a constituent to move (‘b’) that share its index with a node beginning *ICH*- that is immediately under ‘a’. The second part of the disjunction captures quantifier raising that involves a move to a higher layer of structure, with the pattern involving a relation of domination (‘<<’) from a sister of the target position (‘a’).
The action for the first pattern involves inserting a place holder node (PLACE) so that it becomes an immediate right sister of the node named ‘a’.
The actions for the second pattern involve relabelling the ‘a’ node with the main content from the ‘b’ node (that is, the ‘b’ node content minus the index and any material that either comes after the index or before the index but after a semi-colon (;)), relabelling the ‘b’ node as NP together with the content of the ‘b’ node that includes the index and any extra content that either comes after the index or comes before the index but after a semi-colon, followed by movement of ‘a’ to be an immediate left sister of ‘b’, followed by movement of ‘b’ to be an immediate left sister of the place holder (‘x’) inserted with the action of the first pattern, followed by deletion of the place holder ‘x’.
Input:
Output:
deletes <name1> and inserts a copy of <name2> in its place.
replace <name> <tree> <tree2>...deletes <name> and inserts the new tree(s) in its place. If more than one replacement tree is given, each of the new subtrees will be added in order where the old tree was. Multiple subtrees at the root is an illegal Tsurgeon action and will throw an exception.
In Program 11, replacement is of punctuation that begins with three dots by three instances of full stop punctuation.
Input:
Output:
inserts the named node or tree into the position specified. The ways to specify position are:
$+ <name> the left sister of the named nodeThe transformation seen with Program 11 can be achieved more generally with Program 12:
Input:
Output:
creates a subtree out of all the nodes from name1 through name2. The subtree is moved to the foot of the given auxiliary tree, and the tree is inserted where the nodes of the subtree used to reside. If a simple label is provided as the first argument, the subtree is given a single parent with a name corresponding to the label. To limit the Tsurgeon action to just one node, elide name2.
Auxiliary trees must have exactly one frontier node ending in the character ‘@’, which marks it as the ‘foot’ node for adjunction. Final instances of the character ‘@’ in terminal node labels will be removed from the actual label of the tree.
All other instances of ‘@’ in terminal nodes must be escaped (i.e., appear as \@); this escaping will be removed by Tsurgeon.
The first pattern-action pair of Program 13 creates a right binarization of the input tree with the creation of ‘artificial’ non-terminal nodes (ILYR) that span between the second node (‘<2 __=x’) and the end node (‘<-1 __=y’) of a constituent with at least three nodes (‘<3 __’) and that contains a main verb that has a preceding sister (‘< (/^V/ $, __)’).
The second pattern-action pair of Program 13 creates a left binarization of the input tree with the creation of ILYR nodes that span between the first node (‘<1 __=x’) and the second to last node (‘<-2 __=y’) of a constituent with at least three nodes (‘<3 __’).
Input:
Output:
Notably, the output gives the main verb as the most embedded element surrounded by the left binarization of following elements, which in turn is followed by the right binarization of preceding elements.
adjoins the specified <auxiliary-tree> into the specified <target-node>. The daughters of the target node will become the daughters of the foot of the auxiliary tree.
Program 14 has a pattern to find nodes labelled NLYR that have a sister node that is either N or NS. This pattern is paired with an action that replaces the matched NLYR node with an NP node that furthermore has a PP projection and that contains an initial (P-ROLE of) element. There is a second pattern to find nodes labelled PP that have a sister node that is either N or NS. This second pattern is paired with an action that moves the PP node so that it occurs immediately after the matched N or NS node.
Input:
Output:
is similar to adjoin, but preserves the <target-node> and makes it the root of <auxiliary-tree>. The root of the <auxiliary-tree> is ignored.
Program 15 illustrates the addition of an NLYR layer into a noun phrase that dominates a CONJP node.
Input:
Output:
is similar to adjoin, but preserves the <target-node> and makes it the foot of <auxiliary-tree>. The foot of the <auxiliary-tree> is ignored.
The first pattern-action pair of Program 16 adds a ZERO node above terminal nodes that start with ‘*’ and are dominated by an NP node. The second pattern-action pair adds a WORD node above terminal nodes that are not dominated by WORD (thus, ensuring termination), ZERO, or a node that begins with PU.
Input:
Output:
puts a (Penn Treebank style) coindexation suffix of the form ‘-n’ on each of nodes <name_1> through <name_m>. The value of n will be generated in reference to the existing coindexations in the tree, thus avoiding an accidental clash of indices for nodes that are not meant to be coindexed.
The pattern of Program 17 contains two pattern segments (see section 4.6). The first pattern segment matches a node (identified as ‘x’) that: (i) contains a non-empty substring that starts with ‘;{’ and ends with ‘}’ and that is referenced with the variable group name index, (ii) doesn't dominate a PRO node, (iii) is contained within a node (identified as ‘y’) that has CND as a substring (a constituent layer that will be the antecedent of a conditional), and (iv) has a leftmost terminal descendant (identified as ‘a’) that doesn't end within an index string. The second pattern segment matches a node that: (i) contains a non-empty substring that starts with ‘;{’ and ends with ‘}’ and is the same string referenced with the variable group name index of the first pattern segment, (ii) dominates a PRO node, (iii) precedes the node referenced as ‘x’ by the first pattern segment, (iv) is not contained within the node referenced as ‘y’ by the first pattern segment, and (v) has a leftmost terminal descendant (identified as ‘b’) that doesn't end within an index string. When the overall pattern is satisfied an action is triggered to coindex the nodes identified with ‘a’ and ‘b’.
Input:
Output:
While a yield of the input tree gives (64):
a yield of the output tree gives (65):
That is, the change serves to retain the anaphoric link information following a yield.
Clause-level coordination in the Kainoki Treebank is represented by placing the content of clausal conjuncts that are prior to the last conjunct under stacked subordinate IP-ADV nodes that contain a -CONJ extension or that are followed by a conjunction marker (CONJ) (possibly with intervening punctuation) (or both). Program 18 demonstrates how it is possible to transform this coding of clause-level coordination with subordinate structure into a coding that has coordinate structure with CONJP and ILYR (clause internal layer) nodes.
Input:
Output:
Levy, Roger and Galen Andrew. 2006. Tregex and Tsurgeon: tools for querying and manipulating tree data structure. In Calzolari, Nicoletta et al., Proceedings of the Fifth International Conference on Language Resources and Evaluation (LREC'06), European Language Resources Association (ELRA), Genoa, Italy. Available at https://aclanthology.org/L06-1311/.
Pito, Richard. 1994. tgrepdoc–documentation for tgrep. University of Pennsylvania.
Rohde, Douglas. 2005. TGrep2 User Manual version 1.15. Available at: https://github.com/andreasvc/tgrep2.