Figure 1: Notable relationships between nodes
TGrep2 and Tregex are tools for searching syntax trees. This guide introduces their shared query language.
TGrep (Pito 1994) was the original tree-matching command-line program that came with the Penn Treebank. TGrep2 (Rohde 2005) is a TGrep-like implementation that adds extensions to the query language. Tregex (Levy and Andrew 2006) is another TGrep-like implementation that replicates much of the extended search functionality of TGrep2 together with its own extensions. Tregex also offers a desktop application for directly browsing source trees in traditional bracketed (Penn) treebank notation and even offers ways to manipulate trees with its Tsurgeon component. This guide aims to provide an introduction to the extended query language shared by both TGrep2 and Tregex.
Search queries are expressed as patterns that consist of node descriptions to match nodes and relationships establishing links or negated links to other nodes. Notably:
Typically, spaces are optional in patterns. But for readability, it is usually best to place spaces between relationships and node expressions.
Single tree nodes are matched by node descriptions:
If a simple character string or a regular expression begins with an exclamation mark (!), the matching process will be complemented. That is, matches will turn into non-matches, and vice-versa. For example, !VB matches any node that is not VB, and !/^I/ will match any node that does not start with I.
Specified as a string with surrounding slashes (/), a regular expression matches a node if there is a part of the node that is matched. For example, (1) matches sing, singing, amusing, basingstoke, etc.
The caret symbol (^) anchors the regular expression to the beginning of a matched node. So, (2) cannot match amusing or basingstoke but will match sing and singing.
A dollar sign ($) as the last character will anchor the regular expression to the end of a matched node. For example, the caret and dollar-sign in (3) restricts matching to waggle, wiggle and wriggle.
Note how (3) contains round brackets ((, )) which are used to mark a subexpression called a block or capturing group. Within a capturing group the pipe symbol (|) can be used to separate subexpressions with the meaning to match at least one of the subexpressions.
Note, care is needed when writing regular expressions that end with dollar signs. This is because you are forced to predict what the end content of a node could be. For example, suppose you wished for a node description that would match all noun phrase nodes that lack functional extensions (so don't contain subject marking -SBJ, temporal marking -TMP, etc.). In addition to matching nodes that are simply NP, you will also want to match nodes like NP;{BOY}. However, you will not want to match either NP-SBJ or NP-SBJ;{BOY}, since these have subject marking. The regular expression we need is (4).
Note how (4) contains a capturing group that ends with a question mark symbol (?) saying to match its preceding element (the capturing group) one or zero times. Also note how the capturing group contains a dot symbol (.) that is a character wildcard to match any character and a plus symbol (+) saying to match its preceding element (any character) one or more times. In contrast, the semi-colon character (;) will only match itself.
A regular expression can also be constrained with ‘\b’ to mark a word boundary. Thus, (5) will match NP and NP-PRD but will not match NPR.
Word boundary markers are typically used to constrain matching nodes at the constituent level of structure (e.g., /^NP\b/, /^ADVP\b/, /^IP-MAT\b/) and this is generally a good policy to follow. However, you need /^IP-INF/ to match IP-INF, IP-INF2 and IP-INF3 nodes, and you need /^IP-PPL/ to match IP-PPL, IP-PPL2 and IP-PPL3 nodes.
Regular expressions are case sensitive and so (5) and (6) match different nodes.
The star symbol (*) is a metacharacter saying to match its preceding element (any character) zero or more times. To match an instance within a node label of this character or any other metacharacter (“^”, “$”, “.”, “+”), add a backslash (\) as an “escape symbol”. For example, (7) searches for nodes that begin with “*”.
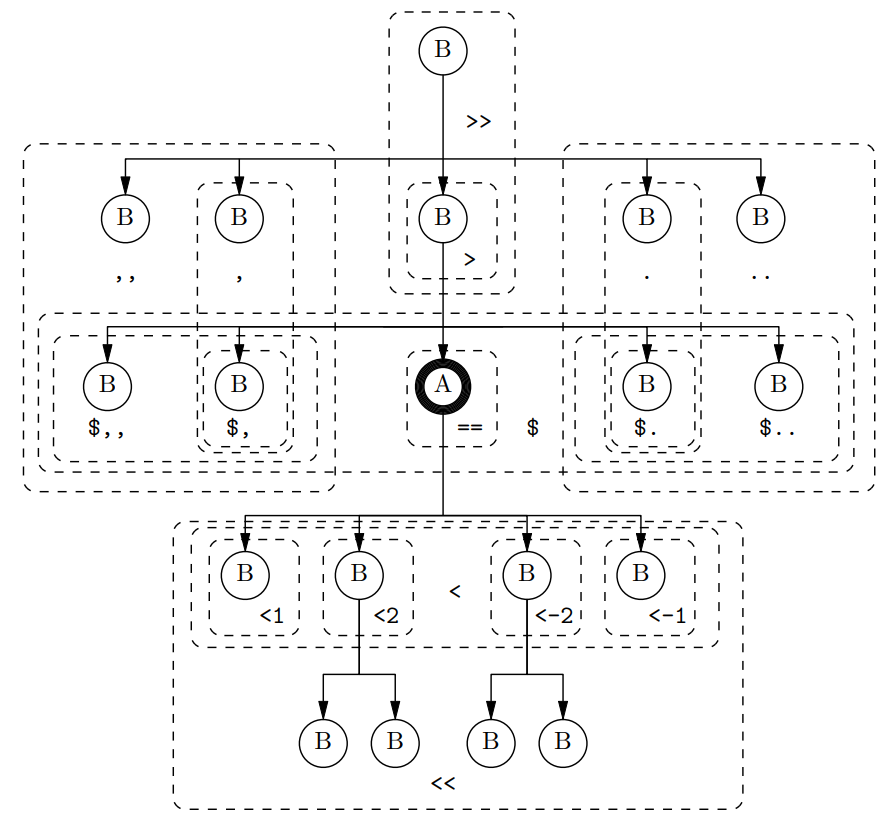
Relationships establish connections between nodes matched by node descriptions. There is a complete pairing of relationships with counterparts, allowing for flexibility choosing the initial node of the pattern when constructing complex relationships (see section 4). Notable relationships can be pictured as in Figure 1.
The relationships pictured in Figure 1 are described in (8). The instances of A and A' in (8) are node descriptions able to match the node labelled A in Figure 1. The instances of B in (8) are node descriptions able to match nodes labelled B in Figure 1.
Any relationship can be negated by immediately preceding it with an exclamation mark (!). Examples of patterns with negated relations are given in sections 3.8, 4 and 5 below.
As a demonstration of paired relations immediately dominates or is immediately dominated by, the wildcard node descriptions (__) in (9) match any node that is immediately under a node labelled IP-INF2.
Tree (10) has a node labelled IP-INF2. The wildcards of (9) match any of the marked nodes in (10) (one match for each search hit) that are not IP-INF2, all of which are situated immediately below IP-INF2, but not any lower.
As a demonstration of paired relations dominates or is dominated by, the wildcard node descriptions (__) in (11) match any node that is under a node labelled IP-INF2.
Tree (12) has a node labelled IP-INF2. The wildcards of (11) match any of the marked nodes in (12) (one match for each search hit) that are not IP-INF2, all of which are situated below IP-INF2.
As another demonstration of paired relations dominates or is dominated by, the wildcard node descriptions (__) in (13) match any node that dominates a node labelled TO.
Tree (14) has a node labelled TO. The wildcards of (13) match any of the marked nodes in (14) (one match for each search hit) that are not TO, all of which are situated above TO.
As a demonstration of paired relations precedes or follows, the wildcard node descriptions (__) in (15) match any node that is preceded by a node labelled flows.
Tree (16) has a node labelled flows. The wildcards of (15) match any of the marked nodes in (16) (one match for each search hit) that are not flows, all of which occur after flows.
As another demonstration of paired relations precedes or follows, the wildcard node descriptions (__) in (17) match any node that is followed by a node labelled flows.
Tree (18) has a node labelled flows. The wildcards of (17) match any of the marked nodes in (18) (one match for each search hit) that are not flows, all of which occur before flows.
As a demonstration of paired relations immediately precedes or immediately follows, the wildcard node descriptions (__) in (19) match any node that is immediately preceded by a node labelled flows.
Tree (20) has a node labelled flows. The wildcards of (19) match any of the marked nodes in (20) (one match for each search hit) that are not flows, all of which occur immediately after flows and no later.
As another demonstration of the paired relations immediately precedes or immediately follows, the wildcard node descriptions (__) in (21) match any node that is immediately followed by a node labelled flows.
Tree (22) has a node labelled flows. The wildcards of (21) match any of the marked nodes in (22) (one match for each search hit) that are not flows, all of which occur immediately before flows and no earlier.
As a demonstration of the sister relation, the wildcard node descriptions (__) in (23) match any node that is a sister of a node with a label that /VBP;~Ipr/ can match.
Tree (24) has a node with a label that /VBP;~Ipr/ can match. The wildcards of (23) match any of the marked nodes in (24) (one match for each search hit) that are not /VBP;~Ipr/ matches, all of which occur at the same level in the tree structure as the /VBP;~Ipr/ match.
As a demonstration of paired relations sister and precedes or sister and follows, the wildcard node descriptions (__) in (25) match any node where a node with a label that /VBP;~Ipr/ matches is a preceding sister.
Tree (26) has a node with a label that /VBP;~Ipr/ can match. The wildcards of (25) match any of the marked nodes in (26) (one match for each search hit) that are not /VBP;~Ipr/ matches, both of which occur at the same level in the tree structure as the /VBP;~Ipr/ match and occur after the /VBP;~Ipr/ match.
As a demonstration of paired relations sister and immediately precedes or sister and immediately follows, the wildcard node descriptions (__) in (27) match the node where a node with a label that /VBP;~Ipr/ matches is the immediately preceding sister.
Tree (28) has a node with a label that /VBP;~Ipr/ can match. The wildcards of (27) match the PP-CLR-DIR node in (28), which occurs at the same level in the tree structure as the /VBP;~Ipr/ match and comes immediately after the /VBP;~Ipr/ match.
To specify the exact child position which a node must (or must not) occupy, use the i-th child relationships (<i, <-i, !<i, and !<-i; also expressed with >i, >-i, !>i, and !>-i). In these relationships, i represents a number indicating which child ‘slot’ is to be considered. Positive numbers are counts from the left edge. Negative numbers are counts from the right edge. For example, pattern (29) finds NP nodes where the second child is an ADVP.
Pattern (30) finds NP nodes where the last child is a PRN.
Pattern (31) finds IP-INF-REL nodes which have less than four children. That is, every IP-INF-REL which has four or more children will have something as its fourth child to make matching with (31) fail.
To match nodes with specific numbers of children, specify both positive and negative i-th child relationships. For example, pattern (32) finds IP-INF-REL nodes which dominate between two and three children.
Other available relationships between nodes, additional to those given above in (8), are given in (33):
Complex Tregex patterns can be constructed by specifying Boolean expressions of relationships that connect to a node. If no operator is placed between two relationships, they are assumed to be connected by an and, which can be specified for clarity with an ampersand (&). Thus, patterns (34) and (35) both match an /^IP-INF-REL\b/ node which immediately dominates a /^PP\b/ node and which dominates an /^IP\b/ node.
The second relationship ‘<< /^IP\b/’ refers to the matched /^IP-INF-REL\b/ node and not to the matched /^PP\b/ node, and is equivalent to (36).
The placement of parenthesis can be used to group a node with its relationship(s), so that (37) will match an /^IP-INF-REL\b/ which immediately dominates a /^PP\b/ which in turn dominates some /^IP\b/.
If a pipe (|) is placed between two relationships, only one of the relationships must be satisfied. Pattern (38) will find an /^IP-INF-REL\b/ node which immediately dominates a /^PP\b/ node or dominates an /^IP\b/ node.
The (possibly implicit) and binds tighter than the or. So pattern (39) will find an /^IP-INF-REL\b/ node that has /^BE\b/ and /^IP-PPL-CAT\b/ children or that has /^BE\b/ and /^NP-PRD2\b/ children.
To create more complex expressions, square brackets ([, ]) can be used to group relationships to form a complex relationship. Thus, pattern (40) finds an /^IP-INF-REL\b/ that has a /PRD/ or /CAT/ child, and that precedes a /^PP\b/ sister or follows an /^ADJP\b/ sister.
Because a square bracketed expression itself acts as a complex relationship connecting to a node, an open square bracket must immediately precede a relationship or another open square bracket that itself starts a complex relationship.
Any relationship, including a square bracketed one, can be negated by immediately preceding it with an exclamation mark (!). Thus, pattern (41) will find /^IP-REL\b/ nodes that have a /^BEP\b/ child while having neither a /CAT/ child nor simultaneously /SBJ/ and /PRD2/ children.
Search patterns allow for a matched node to be given a unique label with an equal sign (=). Once labelled, a node can thereafter be referred back to elsewhere within the search pattern. Such a ‘back link’ is accomplished when the node name only consists of an equal sign and a label, with the label serving to refer to the node that has been assigned to that name elsewhere in the pattern. It is only possible to express patterns in which the labelled node comes prior in the connected structure of the pattern that leads to a back link.
As an example of how back links are useful, consider the task of finding relative clauses with object traces. An object trace might be embedded arbitrarily deeply inside its relative clause, which is captured with the dominates relation (‘<< (/OB1/ < /\*T\*/)’). However, without further qualification, this is too liberal, as it will also allow the return of a relative clause that itself has no object trace but contains a relative clause with an object trace. We can add the extra qualification to prohibit the unwelcome scenario with a back link, resulting in (42).
The added back link statement (‘!>> (/REL/ >> =p)’) requires there to be no intervening relative clause (/REL/) between the object trace and the relative clause that the pattern serves to find.
Search patterns can be split into multiple segments, which are separated by colons (:). Segments following the first have to include a reference to a labelled node that is introduced in a previous segment. Thus, pattern (43) will find trees where an NP immediately dominates a CP-THT.
With labeling of complex nodes, segments can entirely replace patterns that otherwise require embedded relationships. Pattern (44) without segments and pattern (45) with segments match identical structure. For example, they will find the tree of (46).
Levy, Roger and Galen Andrew. 2006. Tregex and Tsurgeon: tools for querying and manipulating tree data structure. In Calzolari, Nicoletta et al., Proceedings of the Fifth International Conference on Language Resources and Evaluation (LREC'06), European Language Resources Association (ELRA), Genoa, Italy. Available at https://aclanthology.org/L06-1311/.
Pito, Richard. 1994. tgrepdoc–documentation for tgrep. University of Pennsylvania.
Rohde, Douglas. 2005. TGrep2 User Manual version 1.15. Available at: https://github.com/andreasvc/tgrep2.